 |
| Physarum polycephalum |
So, obviously all of us
understand the shortest path problem common to computer science. And obviously, we all know about the acelluar
slime mold, Physarum polycephalum. And
that these two things, an algorithmic solution living in the binary world and
an organism living in the physical world, are incredibly and surprisingly
connected.
But
just in case you forgot about these two topics, I’ll refresh your memory.
Researchers claimed in 2000
that that an acellular slime mold, a yellow, sticky, tubular growth shown in
the picture above, solved the shortest path problem, which asks the question,
what is the quickest way to get from one point to another (1)? In the article published in Nature, P. polycephalum determined the shortest
path between two food sources. The
importance of that feat lies in the background of the algorithmic solution to
the shortest path problem, which I will explain first. The cellular machinery behind the biological
solution is incredible, and will be discussed after.
The shortest path problem
lives within the realm of Graph Theory, which is the study of graphs. I know
you’re thinking:
But in this case, you’d be wrong. Graph theory, as it relates to computer
science, is a little different than your standard algebra class where you use a
set of axes to depict functions. In computer science, graphs look like this:
Where the numbered circles
are called nodes and the lines are called edges. The nodes are destinations and the edges are
paths to travel between those destinations.
These graphs are not normally drawn to scale, so weights, represented by
the letters, are added and associate a cost with moving along any given single
or multiple edges. This is similar to
deciding to take the highway or side streets in rush hour. The highway may be more direct, having a
smaller number of edges to traverse, but taking side streets probably saves
time even though the distance is longer.
The shortest path problem
asks a simple question, if weights are additive, what is the shortest path
between two nodes? There are different variations of this question, depending
on what type of problem is being solved.
But for this example, let’s say we are trying to find the quickest path
between nodes 1 and 6.
The first famous algorithm
that tackled this problem was published by Edsger W. Dijkstra in 1959 (2). The solution
is based on two factors; one, the weights of the edges, and two, which nodes
are connected. The algorithm moves systematically through the graph, starting
at node 1, and determines the placement of nodes and edges (2). If the algorithm started at node 1, it would
find two edges emanating from it; edge a to node 5 and edge b to node 2. The algorithm will pick a newly found node,
say node 2, then determine what edges and nodes it has. This continues until the entire graph has
been discovered.
It keeps track of which
nodes it has visited and which nodes it hasn’t in a matrix by saving the weight
of the edge that connects two nodes. If two nodes do not have a connection, the
matrix saves a value of infinity (2). After inputting information gathered from
nodes one and two, the matrix would look like this:
There is also another
matrix that keeps the minimum weight of a path from one node to another. This matrix is a bit more complicated. A
truncated version is shown with possible pathways between node 1 and any other
node. What is shown in the result from
the completion of the program, after the entire graph has been discovered. In
reality, the matrix would compare values for different paths, and only save the
one that was the shortest:
As you can see, the
algorithm gets complicated quickly. The
bigger the graph, the bigger the matrices, and if you’re looking for the
shortest distance between any two given nodes…phew.
Now the question is, did
this slime mold actually solve the shortest path problem?
The answer is yes. Researchers
created a maze and placed small pieces of P. polycephalum throughout and let it grow until the
organism filled it entirely (1). The
figure below shows the maze after this point. Blue lines depict the possible ways the organism could grow to create a path
between the two food sources (which are shown in the figure after this one,
labeled AG), and are labeled by a1, a2,
b1,
and b2.
There are four possible paths through the maze
between the food sources. The slime mold needed to decide which path to take at
two different points; between a1 and a2,
and between b1 and b2. a2
was 22% shorter than a1, and b1 and b2 only had a 2% difference (1). Four hours after the food sources
were placed, the maze looked like this, which shows that only the connections
between the two food sources were kept by leaving growth in all possible
pathway solutions, and any growth leading to dead ends was moved.
Noticing this, the researches left the organism
for another four hours. By maximizing
the solution the organism chose pathway a2b1,
after eight hours which was the best solution to the maze (1).
Researchers
were thrilled, and called this incredible show of “foraging efficiency” a
primitive form of intelligence. Foraging means obtaining food and nutrients,
and completing it efficiently means the organisms fitness increases.
Intuitively, taking the shortest path from the cave to the watering hole is the
most efficient because it saves both time and energy.
So
how does this slimy mold solve a complicated problem in a matter of hours?
It
has to do with its physiology. Because P. polycephalum is acellular, its body
consists of one giant cell, so there are no walls separating one side of the
organism from another. That means that
its contents, including water, nutrients, and proteins, move without being
inhibited. But that does not mean that the movement is not controlled. The slime mold pulsates, like the beating of
a heart, by alternating the direction of water current (3). The water carries with it Calcium ions, which
cause the contraction of the plasma membrane. This is analogous to squeezing a
water balloon or stress ball, where the force that you exert with your hand
causes the object to bulge out. This
contraction and relaxation cycle moves the front edge of the plasmodium forward.
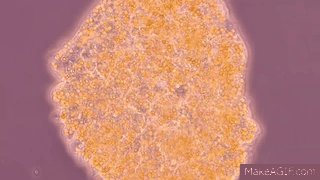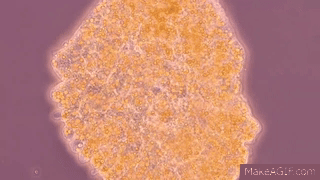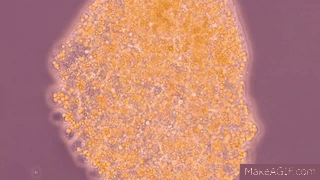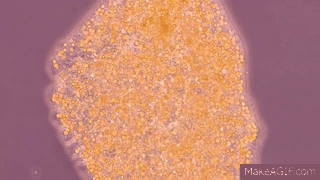
Here
is a gif, adapted from “This Pulsating Slime Mold Comes in Peace (ft. It's Okay
to Be Smart) | Deep Look” YouTube video,
of the cellular contents of the plasmodium sloshing back and forth:
make action GIFs like this at MakeaGif
The
current within the cell can move in any direction, and changes based on the
environment (3). There are two stages to
P. polycephalum movement. The
first is the searching phase, where the majority of the body mass is radiating
outward in a fan shape in search of food (4). After the fan gets big enough,
there is not enough body mass to cover the surface where the fan has been, so
the organism creates veins. Here is a
snapshot from a video that shows four separate droplets of food where P.
polycephalum is consuming the first and searching for more:
 |
| https://www.youtube.com/watch?v=mvBSkt6LhJE |
Once
the protoplasm finds food, the organism enters the second stage of movement,
called the feeding stage (4). Here, almost the entire body mass is moved to the
location of the new food source, seen by it being covered completely with
yellow slime.
When
the food source runs out, the organism moves back to the searching stage, and
fans out, creating veins until it finds its next meal:
The
solution to the shortest path problem lies in the efficiency of the movement
style. As we saw, the protoplasm only
leaves a few thick tubes between food sources. From hydrostatic theory, thicker
tubes are more efficient than thin tubes at passing nutrients (3). Think of it like this, if you needed to put
out a house fire, you wouldn’t try to push water from a fire hydrant through a
straw. And along the same analogy, if
you were putting out a house fire, you would use the fire hydrant that was
closest, rather than running the fire hose down another block. By having thick and short pipes, the organism
solves the seemingly complex shortest path problem, simply by maximizing its
efficiency.
So,
now what?
We’ve
learned about the algorithm that answers the question, what is the shortest
distance between two places given a bunch of different paths? And we’ve learned that life, compact in a
slime mold, solves the exact same problem without storing tables of numbers. Though the shortest path problem is an
interesting intellectual endeavor for humans, the shortest path problem is life
or death for this organism, and it seems to understand intuitively that the
shortest path between two points maximizes its likelihood of surviving. Because of this amazing feat, researchers
study Physarum polycephalum to understand the
fundamentals of what makes life, alive.
References
1.
Nakagaki T, Yamada H. 2000.
Maze-solving by an amoeboid organism. Nature 407:470.
2.
Dijkstra EW. 1959. A
note on two problems in connexion with graphs. Numerische Mathematik 1:269–271.
3.
Nakagaki T, Kobayashi R, Nishiura Y,
Ueda T.
2004. Obtaining multiple separate food sources: behavioural intelligence in the
Physarum plasmodium. Proceedings of the Royal Society B: Biological Sciences 271:2305–2310.
4.
Halvorsrud R, Giaever I, Feder J. 1997.
Growth and Synchronization of Physarum Plasmodia on a Lattice of Disconnected
Nutrient Drops. Biological Rhythm Research 28:358–364.











This comment has been removed by a blog administrator.
ReplyDeleteThanks for sharing, nice post! Post really provice useful information!
ReplyDeleteAn Thái Sơn với website anthaison.vn chuyên sản phẩm máy đưa võng hay máy đưa võng tự động tốt cho bé là địa chỉ bán máy đưa võng giá rẻ tại TP.HCM và giúp bạn tìm máy đưa võng loại nào tốt hiện nay.